Introduction

A fundamental result of diffusion theory is that the mean path length of particles diffusing across a certain region of space is entirely independent of the characteristics of the diffusion process1,2,3. In fact, only the shape of the outer boundary of this region determines the average length of particle trajectories between entering and exiting this region; whether the paths taken by the particles are straight lines or convoluted random walks is, however, completely irrelevant. As such, this mean path length invariance generalizes the so-called mean chord length theorem valid in the ballistic limit2 and encompasses applications in basically all research fields where diffusion processes or random walks arise—ranging from nuclear physics1 and solar energy harvesting4 to the movement of bacteria5.

The scope of this invariance property was recently expanded even further, when it was shown that not only particles, but also waves that scatter through a region of space are subject to the same invariance property6. The key insight here is that the average time-delay associated with a scattering process is directly linked to the density of states (DOS) inside the scattering region7,8,9,10. From the Weyl law11,12 we then know that the DOS remains invariant when transforming a homogeneous medium in the ballistic limit into a diffusively scattering disordered medium of the same size6. A recent experimental implementation followed exactly this line of thought by changing the turbidity of a liquid from nearly transparent to very opaque and demonstrated that the mean path length of isotropically incoming light inside the liquid stays, indeed, unchanged over nearly two orders of magnitude in scattering strength13. In spite of its coherent nature, laser light could thus be observed to obey the same universal invariance property as particles when scattering ballistically or diffusively.

Coherent wave effects can, however, also lead to very strong deviations from any of the transport regimes that particles can be in. Consider here, e.g., the regime of Anderson localization14,15 or the formation of a band gap in a photonic crystal16, to cite just two genuinely wave-like phenomena that both rely on wave interference. The natural question to ask at this point is whether any such effects going beyond a trajectory-based description may lead to a violation of the mean path length invariance since they clearly fall outside the scope of both the mean chord length theorem and a random walk picture. More specifically, since both Anderson localization and a band gap prevent incident waves from propagating inside the scattering region, one naturally expects that the mean path length invariance should break down in these cases. Numerical simulations of the scattering matrix6 suggest that the invariance property may also hold in the localized regime. This is confirmed by the reconstruction of the DOS from measurements of the transmission matrix17. None of these studies however explore the impact of absorption on the estimation of the mean path length. Moreover, the experimental setup used in the latter study does not make it possible to verify the invariance in the ballistic and diffusive regimes as well as for a photonic crystal in which cases a complete measurement of the transmission matrix is required.

Insights into such questions are not just of academic interest: consider, e.g., that the mean path length invariance is strongly linked to the so-called Yablonovitch limit that imposes a cap on the optimal intensity enhancement inside solar cells18. A break-down of the invariance property may thus also provide a strategy for overcoming current limitations in solar cell design4.

Here we will address these questions through an experiment that gives us direct access to these scattering regimes beyond both the ballistic and the diffusive limit. We test the invariance of the mean time-delay in microwave measurements using a multichannel cavity for which the scattering strength of a random sample can be tuned by changing the number of scatterers within the cavity and for which an ordered arrangement of the scatterers mimics a photonic crystal.

The scattering region is formed by an effectively two-dimensional cavity (see "Methods") of length L = 0.5 m and width W = 0.25 m with two arrays of N = 8 antennas attached on the left and right interfaces, respectively19. The antennas are single-mode waveguides fully coupled to the cavity between 11 and 18 GHz (see Fig. 1a). Having full control over all these waveguides enables the measurement of the frequency-dependent N ×N transmission matrix (TM) t b a (ω), which contains the complex and flux-normalized transmission coefficients between the two arrays. The TM is complete, but strong internal reflections occur at the left and right interfaces of the cavity as the spacing between two adjacent antennas is metallic (unlike in open waveguides).

Fig. 1: Experimental setup and path length spectra.
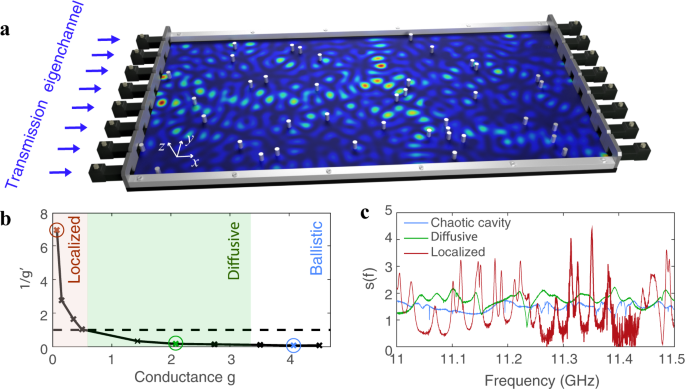
figure 1

a Sketch of the experimental setup, where the cavity is represented for a random arrangement of 40 aluminum cylinders. The top plate has been removed to visualize the interior of the sample. The embedded intensity distribution corresponds to the highest transmitting transmission eigenstate in this scattering configuration obtained from a numerical simulation. b Experimental data for the variation of the inverse of the statistical conductance, \((1/g^{\prime} )=3{\rm{var}}({s}_{a})/2\) as a function of the conductance g to estimate whether the experiment operates in the diffusive \([(1/g^{\prime} )\,<\,1]\) (green shaded area) or in the localized regime \([(1/g^{\prime} )\,> \, 1]\) (red shaded area)21. c Spectra of the mean path length s(ω) =s[2Q t (ω)] for a chaotic cavity (blue line), a diffusive sample with n scat = 100 scatterers (green line) and a localized sample with n scat = 280 scatterers (red line). The values of \(1/g^{\prime}\) corresponding to these samples are shown with red, green and blue markers in (b).

Full size image

To induce a transition from the ballistic to the chaotic, diffusive and the localized regime we gradually increase the scattering strength within the cavity. Specifically, we measure the transmission matrix t(ω) for an empty cavity (ballistic system), for a cavity with an aluminum semicircle of 53 mm diameter [chaotic system, see Supplementary Note 1 for details] and for disordered samples with n scat randomly distributed aluminum cylinders of radius r s = 3 mm. For the disordered systems the conductance \(g=\langle {{{\Sigma }}}_{n = 1}^{N}{\tau }_{n}\rangle\) (i.e., the frequency-averaged sum of transmission eigenvalues τ n of t † t) ranges over more than two orders of magnitude from 4.36 for the empty cavity to 0.01 for the sample with the strongest disorder (n scat = 280).

Because of dissipation within the system and strong internal reflections, the scaling of the conductance g may not reflect the crossover from diffusive to localized waves found at g = 1 in open random systems20. We exploit instead the statistics of the transmitted intensity as a reliable indicator of the localization transition even in the presence of absorption21. Specifically, the variance of the normalized total transmission s a  =T a /〈T a 〉, with T a  = Σ b ∣ t b a ∣ 2, is given for non-dissipative diffusive samples by var(s a ) = 2/(3g). In the case of finite dissipation the so-called statistical conductance \(g^{\prime} =2/[3{\rm{var}}({s}_{a})]\) has been found to indicate localization reliably when taking on values \((1/g^{\prime} )\,> \, 1\) 21. In Fig. 1b, we thus show the change of \(1/g^{\prime}\) with the conductance g and observe values for \((1/g^{\prime} )\) that considerably exceed 1 for g < 0.6. This confirms that the increased disorder in our two-dimensional system leads to wave localization.

In multichannel systems, the mean path length can be estimated from measurements of the Wigner-Smith (WS) time-delay operator Q = −i S −1∂ ω S applied to the scattering matrix S which relates incoming and outgoing channels22,23,24,25,26,27,28,29,30. The operator Q is a multichannel generalization of the phase derivative dϕ b a /dω, which provides the time-delay of a spectrally narrow pulse between two channels a,b. Averaging over all channels leads to the mean Wigner–Smith time-delay given by \({\bar{t}}_{{\rm{WS}}}(\omega )={\rm{Tr}}[Q(\omega )]/(2N)\).

In principle, estimating the mean time-delay requires a measurement of the complete scattering matrix S(ω) including the two reflection matrices on the left and right sides of the sample, respectively. Experimentally, such a measurement is highly challenging, however, since most setups provide access either only to a one-sided reflection matrix or to the TM. To overcome this difficulty, we show in Supplementary Note 2 that the trace of Q(ω) and the trace of the Wigner-Smith operator involving only the TM from left to right, Q t (ω) = −i t −1∂ ω t, are connected through the following equivalence relation:

$$s[Q(\omega )]=s[2{Q}_{t}(\omega )]\,,$$

(1)

where \(s({\mathcal{O}})={c}_{0}{\rm{Re}}[{\rm{Tr}}({\mathcal{O}})/(2N)]\) is the mean length obtained with an operator \({\mathcal{O}}\). The above simple relation, which extends the decomposition of the DOS into a superposition of contributions from each transmission eigenchannel17, is proven in Supplementary Note 2 for non-absorbing systems. The key ingredient is the correspondence between transmission and reflection eigenchannels as a consequence of the unitarity of the scattering matrix, S(ω)S †(ω) =\({\mathbb{1}}\) 17,31. The transmission eigenchannel time-delay \({t}_{n}^{(t)}(\omega )={\rm{d}}{\theta }_{n}/{\rm{d}}\omega\), found from the derivative of a composite phase shift θ n of the singular vectors of the TM17, is then equal to the average of the corresponding reflection delay times at the right and left sides of the sample, \({t}_{n}^{(t)}(\omega )=[{t}_{n}^{(r)}(\omega )+{t}_{n}^{({r}^{\prime})}(\omega )]/2\) (as in 1D systems32), where a prime denotes the quantities at the other waveguide port. Equation (1) thus provides access to the mean path length \(s[Q(\omega )]={c}_{0}{\bar{t}}_{{\rm{WS}}}(\omega )\) through transmission measurements only.

Measuring the complete TM between single-mode waveguides, as opposed to a sub-part of it with a grid of points at the input and output of a tube17, opens the door to an accurate estimation of the mean length not only in the localized regime but also in the ballistic and diffusive regimes. In practice, evaluating s[2Q t (ω)] requires that eigenchannels of t(ω) with small transmission eigenvalues τ n (typically τ n  < 10−6) are removed from the experimental data since these eigenchannels may contain time-delays \({t}_{n}^{(t)}(\omega )\) that are corrupted by the noise level of the experimental setup. In diffusive and localized systems, eigenchannels with the smallest transmission values are typically associated with a small intensity build-up inside the medium and therefore with small time-delays17. Removing their contribution to s[2Q t (ω)] thus modifies the estimated length only weakly (see Supplementary Note 5).

Spectra of the mean path length s[2Q t (ω)] corresponding to a chaotic cavity, a diffusive sample and a localized sample, are presented in Fig. 1c. In contrast to the diffusive regime in which the overlap of many resonances leads to small fluctuations of s[2Q t (ω)], the peaks observed in the localized regime correspond to the contributions of spectrally isolated resonances associated with localized modes. To meaningfully compare the mean path length obtained in the different propagation regimes, it is thus necessary to average s[2Q t (ω)] over a frequency range containing several of these peaks.

Results and discussion

Disordered systems

In Fig. 2 we compare the mean path length 〈s(2Q t )〉 resulting from a frequency-average in single configurations (see Methods) with the theoretical predictions obtained using the Weyl law6,11,12 given by

$${s}_{{\rm{theo}}}(\omega )=\frac{1}{2N{c}_{0}}\left(\omega A+\frac{C-B}{2}{c}_{0}\right)\ .$$

(2)

This Weyl prediction for the mean path length involves the scattering area \(A=LW+16lw-{n}_{\text{scat}}\pi {r}_{{\rm{s}}}^{2}\) corresponding here to the surface of the cavity, including the attached channels of length l = 38 mm and aperture w = 15.79 mm, from which the area of the impenetrable metallic scatterers is subtracted. A first-order correction term takes into account the external boundaries C = 16w and the internal boundaries B of the scattering system, that include the metallic boundaries of the cavity and the circumferences of the metallic cylinders6. Smaller values of g are reached with an increasing number of these cylinders, which reduces the effective scattering area and increases the length of the internal boundaries. The theoretical estimate of the mean path length 〈s theo(ω)〉 is then the average of s theo(ω) over the frequency range and decreases from 2.05 m for an empty cavity to 1.76 m for a sample with 280 cylinders. The theoretical mean path length for an empty cavity 〈s theo(ω)〉 ~ 4L strongly exceeds its value for open waveguides 〈s theo(ω)〉 =π L/26. This enhancement is due to the metallic spacings between the antennas at the right and left interfaces of the cavity. Numerical simulations presented in Supplementary Fig. 2 also show the existence of states with very long delay times in the empty cavity, corresponding to path lengths of a few hundred meters. These states are caused by bouncing orbits between the top and bottom interfaces of the cavity (in the y-direction).

Fig. 2: Mean path lengths with respect to the number of scatterers.
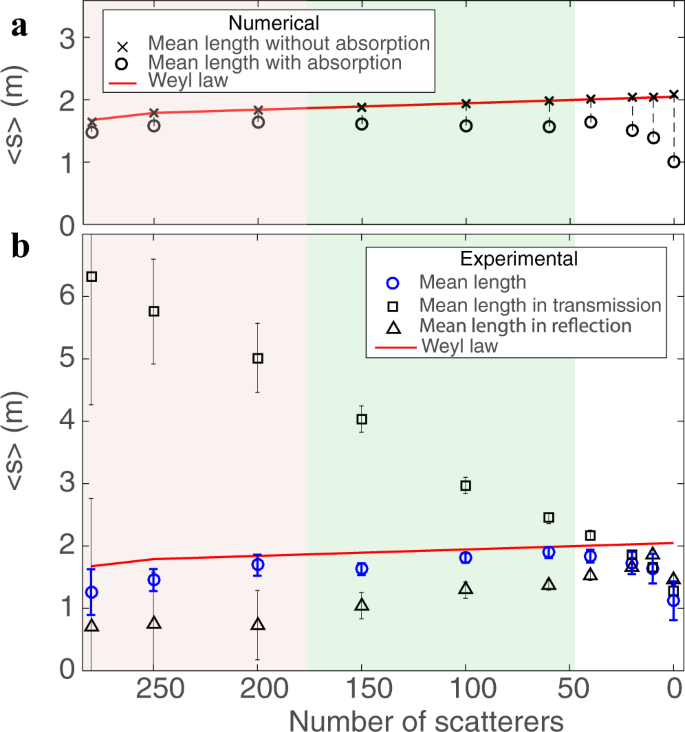
figure 2

a Mean path length evaluated as 〈s(2Q t )〉, see Eq. (1), obtained in simulations without (black crosses) and with (black circles) absorption as a function of the number of metallic cylinders within the cavity. The red solid line is the theoretical length calculated from the Weyl law (see Eq. (2)). Absorption reduces the estimated mean path length. Background colors in rose, green, and white mark the localized, diffusive, and the ballistic regime as in Fig. 1b. b The same quantity, 〈s(2Q t )〉, found experimentally (blue circles). The squares and triangles are the mean path length in transmission and in reflection, respectively (see Supplementary Note 1 for details). Error bars represent the standard deviation.

Full size image

 Figure 2a shows perfect agreement between the Weyl prediction (red line) and the mean path length 〈s(2Q t )〉 obtained in numerical simulations (black crosses) of the experimental setup in absence of absorption (see Methods). Even the small reduction in the mean path length predicted for an increasing number of scatterers is well reproduced. This confirms the validity of the mean path length invariance across the onset of the localization transition.

Also the experimental data shown in Fig. 2b (blue circles) are in good agreement with 〈s theo(ω)〉. How non-trivial this invariance property is, can be appreciated when contrasting it with the strong enhancement (reduction) of the transmission (reflection) time-delays across the localization transition (blue squares and triangles). We also observe that the mean path length is slightly underestimated, especially in the ballistic regime, which can be attributed to the presence of absorption.

Influence of absorption

Even though the DOS integrated over frequency is independent of absorption33, the presence of absorption within the cavity makes the scattering matrix sub-unitary34 and leads to a violation of the mean path length invariance6 so that this deviation comes as no surprise. Indeed, the experimental data are well reproduced by numerical simulations when dissipation is included. For the data shown in Fig. 2a (black circles), we introduce uniform absorption by adding an imaginary part to the effective refractive index of the cavity. We here use for the empty cavity as well as for all disorder configurations an average uniform imaginary part of the refractive index (n i  = 2 × 10−4) found by comparing the frequency-averaged transmission measured for the empty cavity with the numerical simulations.

In addition to its detrimental effect on the mean path length invariance, dissipation also breaks the unitarity of S and therefore the correspondence between s[Q(ω)] and s[2Q t (ω)] in Eq. (1). In the diffusive regime, all of these effects are sufficiently weak such that losses through outgoing channels dominate over uniform absorption over the sample. From the broadening of the average linewidth with respect to the number of ports connected to the cavity, we estimate that the ratio of losses through ports relative to uniform losses within the cavity is equal to 5.4 (see Supplementary Note 3). With the scattering matrix then still being sufficiently close to unitarity, 〈s(2Q t )〉 provides a reliable estimator of the theoretical value 〈s theo〉 in absence of absorption. Interestingly, the stronger deviations found for the empty cavity are a consequence of very specific states that bounce many times between the top and bottom cavity boundary (in the y-direction). Due to their long cavity dwell times, these states are very strongly affected by dissipation and therefore lead to significant deviations from the mean path length invariance (see Supplementary Note 3). The existence of these states is reflected by the large fluctuations of the mean path length in Fig. 2. In the diffusive regime, the disorder scattering naturally leads to a suppression of such states with strongly enhanced time-delays and thereby to a better agreement with the theoretical predictions.

Surprisingly, we observe that our estimate for the mean path length, 〈s(2Q t )〉, is more robust to absorption in the localized regime than in the empty cavity even though Anderson localization also gives rise to the large time-delays in the cavity and large fluctuations of the mean path length (see Fig. 2b). Using a toy model, we demonstrate analytically in Supplementary Note 4 that in the limit of strong absorption s[2Q t (ω)] converges towards the most direct path in transmission 〈L direct〉. As shown in Fig. 3, all eigenchannels feature a quasi-ballistic propagation in this limit providing the same contribution to the mean path length. In this way, the flux in the empty system (with n i  = 10−2, see Supplementary Fig. 6) becomes almost perfectly aligned with the x-direction from left to right as strong absorption suppresses all longer paths35. Indeed, the resulting estimate for the most direct path \(\langle {L}_{{\rm{direct}}}^{{\rm{empty}}}\rangle \approx 0.31\langle {s}_{{\rm{theo}}}\rangle\) is in very good agreement with the numerical value of 〈s(2Q t )〉 = 0.32〈s theo〉. In the localized regime, the presence of metallic and hence impenetrable scatterers elongates the direct path, which is found to be comparable to the mean path length (〈s(2Q t )〉 = 0.66〈s theo〉 for the sample with 280 scatterers and n i  = 10−2). The increased absorption-stability of the mean path length in the localized regime as compared to the ballistic regime is thus explained by the difference in the most direct scattering contributions in these two cases. We emphasize that this robustness of s[2Q t (ω)] in the localized regime is in stark contrast to the much stronger dependence on absorption we observe for a corresponding estimate using the full Wigner-Smith matrix s[Q(ω)] (see Supplementary Fig. 6). Q(ω) contains the full scattering matrix and thus depends on the sum of phase delay times of both transmitted and reflected waves36. In analogy to our analysis from above, the strong absorption reduces these contributions to those coming from the shortest possible paths. However, since the shortest paths contributing here are those that are directly reflected when entering the cavity, their extremely short time-delay values will dominate in the strong absorption limit (see Supplementary Note 4). Compared to transmission eigenchannels whose direct paths have to traverse the whole system, the convergence of s[Q(ω)] to the direct paths in reflection leads eventually to a pronounced underestimation of the mean path length for strongly scattering samples.

Fig. 3: Influence of absorption.
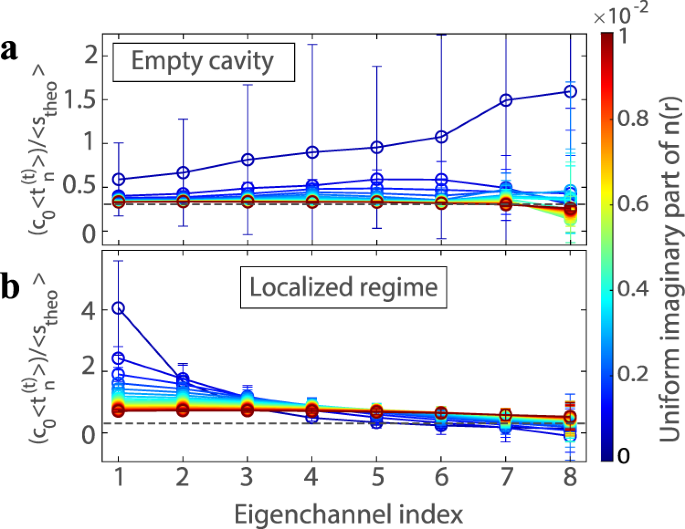
figure 3

a, b Normalized transmission eigenchannel contribution to the mean path length as a function of the index n, where n = 1 (n = 8) corresponds to the highest (lowest) transmitting eigenchannel for the empty sample (a) and a localized sample (b). Increasing absorption leads to a redistribution of the transmission time-delays which all converge to the length of the most direct path in the limit of strong absorption (see Supplementary Note 4). The horizontal black dashed line marks an estimation of the most direct path in the empty system. Error bars represent the standard deviation of the channel delay times in transmission for each eigenchannel.

Full size image

Photonic crystal

After having explored the validity of the mean path length invariance in the crossover to very strong disorder, we will now consider the opposite limit of a structured medium with periodic order. For this purpose, we form a photonic crystal (PC) by a periodic arrangement of alternating aluminum and Teflon cylinders (see Methods). The structure with 15 layers of scatterers in logitudinal direction exhibits a band gap centered at f 0 = 12 GHz with a width Δf 0 ≈ 2 GHz as can be seen in Fig. 4a. Because the PC only fills the middle part of the entire scattering area of the cavity, the mean path length includes the contribution of the PC as well as the free space between the PC and the interfaces of the cavity. To isolate the impact of the PC, we subtract the theoretical free space contribution to s[2Q t (ω)], except in the band gap for which the transmission remains in the noise floor of the experimental setup (≈10−6) and we set s[2Q t (ω)] = 0.

Fig. 4: Path lengths in a photonic crystal.
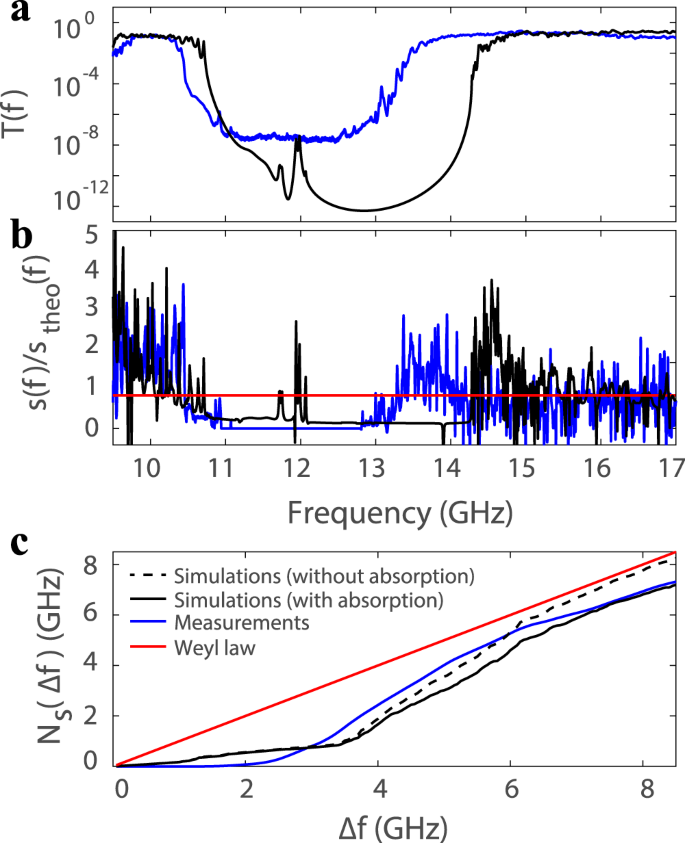
figure 4

a, b Frequency spectra (a) of the transmission and (b) of the mean path length in a photonic crystal obtained in measurements to which the free space contribution has been removed outside the band gap (blue line) and in simulations with absorption (black line). A transmission band gap is clearly observed for this sample with 15 longitudinal layers of regularly spaced scatterers. c Integral of the mean path length normalized by its theoretical value over a frequency window spanning Δf around the center of the band gap. The black dashed line is the result of simulations in absence of absorption. The decrease of the mean path length within the band gap is followed by a strong enhancement starting at the band edges such that the frequency-averaged value progressively converges towards the theoretical Weyl prediction. The experimental data (blue solid line) shows the same trend, but stays slightly below the Weyl prediction for large Δf due to absorption (see agreement with the simulations including absorption, black solid line).

Full size image

Numerical simulations are then performed in a cavity whose scattering region has the same dimensions as the PC with small disorder in the scatterer positions and absorption being added to mimic the situation in the experiment (see Methods). The central frequency of the band gap is now f 0 = 12.6 GHz with a width of 3.3 GHz, which is larger than in measurements. We attribute these differences to tiny air gaps between the top plate and the aluminum cylinders in the experimental setup, where scattering at the top cylinder edge causes the excitation of evanescent modes. The effective properties of the scatterers are thus modified locally due to the coupling of such evanescent modes to neighboring Teflon scatterers. The mean path length is also strongly reduced within the band gap in simulations (see Fig. 4b), but s[2Q t (ω)] is not vanishing as a consequence of the finite length of the PC. We also note that the dwell time can be negative as a result of absorption37 and since the dwell time operator is related to the time-delay operator and thus also to s[2Q t (ω)], this explains the negative values in Fig. 4b.

From such an observation one may be tempted to conclude that the mean path length invariance does not hold in such periodic systems. Following prior theoretical work on frequency sum rules33,38, we know, however, that in a sufficiently broad spectral window, reductions and enhancements of the DOS should compensate each other in arbitrary systems including the case of photonic band gap materials. Due to the connection between the DOS and the mean path length, we should find, correspondingly, that the strong decrease of s[2Q t (ω)] within the band gap is compensated by a corresponding enhancement right outside of the band gap. As can be seen in Fig. 4b, we indeed observe such an enhancement of the mean path length close to the band edges, with values for s[2Q t (ω)] even exceeding 3s theo(ω) in measurements and in simulations.

In Fig. 4c we now show the mean path length normalized by the Weyl prediction, s[2Q t (f)]/s theo(f), integrated over a frequency window Δf centered around the middle of the corresponding band gap f 0 obtained in the experiment or the simulation, \({N}_{s}({{\Delta }}f)=\mathop{\int}\nolimits_{f0-\frac{{{\Delta }}f}{2}}^{f0+\frac{{{\Delta }}f}{2}}\ s[2{Q}_{t}(f)]/{s}_{{\rm{theo}}}(f)\ {\rm{d}}f\). The Weyl law prediction for this quantity is N s (Δf) = Δf. Note that the band gap is not located in the center of our frequency range. Thus, once the lower end of the integration frequency window has reached 9.5 GHz, we continue the integration with only the higher frequency range. In the experiment, this average ratio N s (Δf) now almost vanishes for a spectral window Δf smaller than the width of the band gap but then increases rapidly and progressively converges towards N s (Δf) ≈ 0.86Δf as Δf = 8.5 GHz. As in the case of the empty system or the disordered configurations, this 14% deviation from the Weyl law is due to absorption within the sample. This is confirmed by simulations without absorption for which N s (Δf) indeed reaches N s (Δf) ≈ 0.975Δf. The convergence of N s (Δf) now demonstrates that the pronounced enhancements of s[2Q t (ω)] at the edges of the band gap compensate the vanishing mean path length within the band gap. The fact that we observe the experimental data and the simulations with absorption to converge towards the same value of N s for large Δf in spite of the different band gap sizes for these two cases, further substantiates the invariance property of the mean path length.

Conclusion

In summary, we experimentally demonstrated with microwave measurements that the knowledge of the transmission matrix alone provides a robust way of estimating the invariant mean path length, even in scattering systems with strong wave-interference and weak absorption. Our results clearly show that this invariance property reaches far beyond the diffusive regime and thus provides a comprehensive bound on enhancement of the mean path length of broadband light in a medium.

Methods

Experimental setup

Sixteen antennas that are waveguide-to-coax adapters operating in the Ku-band are attached to the system and fully coupled to the cavity between 11 and 18 GHz. We operate in a frequency window smaller than c 0/2h = 18.75 GHz where only the fundamental mode in the vertical z-direction is excited, making the cavity effectively two-dimensional. Measurements of the frequency spectra of the TM are carried out with two ports of a vector network analyzer connected to two N × 1 electro-mechanical switches to successively excite each transmitting and receiving antenna. The ports of the switches that are not excited are terminated with 50 Ω loads so that the antennas mimic absorbing boundary conditions. The metallic spacing between adjacent antennas generate strong internal reflections at the interfaces of the cavity. The TM is measured between 11 and 13 GHz in the ballistic and diffusive regimes and between 11 and 12 GHz in the localized regime, with frequency steps of 0.4 MHz.

Photonic crystal

The period of the square lattice between a metallic and a dielectric Teflon scatterer is d = 1.2 cm in both the longitudinal and transverse direction. A picture of the experimental setup is shown in Supplementary Fig. 1. The photonic crystal consists of 15 longitudinal layers of scatterers. The variations of the theoretical mean path length s theo(ω) with frequency for a sample of 300 cylinders is given by Eq. (2), where the area of the Teflon cylinders has to be multiplied with their refractive index squared to account for the increased DOS in dielectric materials.

Numerical simulations

We solve the two-dimensional scalar Helmholtz equation \(\left[{{\Delta }}+{n}^{2}({\bf{r}}){k}_{0}^{2}\right]\psi ({\bf{r}})=0\) using a finite element method39,40 (https://ngsolve.org). Here, Δ is the Laplacian in two dimensions, n(r) is the refractive index distribution, r = (x,y) is the position vector, k 0 = 2π/λ is the vaccum wavenumber and ψ(r) is the z-component of the TE-polarized electric field. In our simulations we use the exact dimensions of the experimental setup (see Fig. 1), where the single mode leads are terminated with perfectly matched layers which absorb the outgoing waves without any back-reflections and thus mimic semi-infinite leads. To account for the global losses in the experiment, we add a frequency-independent uniform imaginary part of 2 × 10−4 to the effective refractive index of the cavity which yields the same frequency-averaged transmission in the empty system as in the experiment.

In the case of the disordered systems, we use—just like in the experiment—a single random configuration for each number of scatterers and average the calculated mean path lengths in the range of 11–13 GHz (11–12 GHz for 280 scatterers).

The simulations of the photonic crystal are performed in the frequency interval of 9.5–17 GHz. To mimic experimental uncertainties, we introduce a slight disorder to the positions of the scatterers, i.e., we displace scatterers in the transverse and longitudinal direction by a random value drawn from the interval [−r s/10,r s/10]. We then define our band gap as the frequency interval in which the transmission in the numerical simulation reaches the experimental noise floor (≈10−6).

To calculate the time-delay operators Q, Q t , Q r and \({Q}_{{r}^{\prime}}\) we have to invert the corresponding scattering, transmission or reflection matrices. Since these matrices can be singular, we perform a singular value decomposition and project our matrices onto subspaces containing only singular vectors corresponding to singular values greater than 10−10 which enables us to compute their pseudo-inverse41,42.